Turaganga: Difference between revisions

From All Skies Encyclopaedia
Turaganga
No edit summary
No edit summary
 
(3 intermediate revisions by the same user not shown)
Line 19: Line 19:
Since the Greek period in the forth century CE, Indian astral science used not only the older (Vedic) division of the observable "path of the moon" into 27 nakṣatras, but adopted also the Graeco-Roman division into twelve equal sections called Rāśi (राशिः), equalling the traditional zodiacal signs. A rāśi (राशिः) or zodiacal sign is a section of 30° alongside the ecliptic. Since (Greek) antiquity, ecliptic longitudes are typically not counted from one to 359, but are given as "zodiacal sign ''xy''" or "rāśi ''xy''", where 0 ≤ ''xy'' ≤ 30.
Since the Greek period in the forth century CE, Indian astral science used not only the older (Vedic) division of the observable "path of the moon" into 27 nakṣatras, but adopted also the Graeco-Roman division into twelve equal sections called Rāśi (राशिः), equalling the traditional zodiacal signs. A rāśi (राशिः) or zodiacal sign is a section of 30° alongside the ecliptic. Since (Greek) antiquity, ecliptic longitudes are typically not counted from one to 359, but are given as "zodiacal sign ''xy''" or "rāśi ''xy''", where 0 ≤ ''xy'' ≤ 30.


Therefore, the statement "Mina 2|30" equalling 2.5° of the twelfth Rāśi, means we need to add 11x30=330 and 2.5° to obtain the ecliptic longitude λ=332.5° or ''dhruvaka''=332|30. This is not corrected for precession.
Therefore, the statement "Mina 2|30" equalling 2.5° of the twelfth Rāśi, means we need to add 11x30=330 and 2.5° to obtain the ecliptic longitude ''λ''=332.5° or ''dhruvaka''=332|30. This is not corrected for precession.


For the ''vikṣepa'' (polar latitude measured along the hour circle) is 19|0 N.
For the ''vikṣepa'' (polar latitude measured along the hour circle) is 19|0 N.
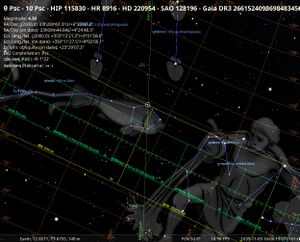
[[File:TetPsc+alfPeg stellarium.jpg|thumb|Stellarium map of the region in question with tet Psc in the centre and naksatra and rasi displayed (SMH 2025).]]
If 19.0 is the ecliptic latitude, the star α Peg would have the correct latitude and the longitude of 332.5° would point to a date of measurement in 488/ 489 CE (1200 years prior to Nityānanda' star catalogue). If 19.0 is measured along the hour circle, only zeta Peg would have the correct latitude, but the longitude of 341° in 1639 CE would point to a date of the measurement of 1019 CE.
{| class="wikitable"
{| class="wikitable"
|+
|+
Line 28: Line 30:
!ecliptic latitude β
!ecliptic latitude β
! rowspan="2" |source
! rowspan="2" |source
!Indian Name
|-
|-
!''dhruvaka''
!''dhruvaka''
!''viksepa''
!''viksepa''
!
|-
|-
|Turaganga
|Turaganga
Line 36: Line 40:
|19°
|19°
|Nityānanda
|Nityānanda
|
|-
|-
|
|
Line 41: Line 46:
|
|
|
|
|
|-
|α Peg
|348.5
|19.5
|Stellarium (1639)
|Ajapāda
|-
|-
|θ Psc
|θ Psc
|350°
|350.2
|9°
|9°
|Stellarium
|Stellarium (1639)
|
|-
|-
|α Peg
|ζ Peg
|348.5°
|341°
|19.5°
|17.75°
|Stellarium
|Stellarium (1639)
|
|-
|γ Peg
|
|
|
|Ahirbudhnya
|}
|}
Stellarium gives the value 350 degrees for the same epoch. The difference can be attributed to the precession correction.
For fixing the coordinates we use the nearest bright stars identified without ambiguity as shown in the chart - Ajapāda Alpha Pegasus and Ahirbudhnya Gamma Pegasus.


===Transfer and Transformation of the Constellation===
===Transfer and Transformation of the Constellation===


Latest revision as of 14:47, 4 November 2025


Turagānga () is an Indian name that occurs in a 17th century star catalogue. Most likely, it refers to a body part of the ancient Greek constellation of Pegasus.

Concordance, Etymology, History

Turgānga means a body part (anga, ) of the horse (turaga, ).

Spelling Variants

  • Turagānga
  • Turangaasa

Origin of Constellation

The name is listed in a 17th century star catalogue by Nityānanda in the work Siddhāntarāja (1639 CE).[1]

The verse provides the coordinates with numbers coded as sārdhadvaya (two and a half) and gobhūmi (19)

Half of a degree added to two degrees 2|30 [is one of the coordinates of] the star Turagānga which shines with second order brightness along the north [latitude] as nineteen degrees 19|0.

It is mentioned in the twelfth Rāśi (राशिः), Mina (Pisces).

Since the Greek period in the forth century CE, Indian astral science used not only the older (Vedic) division of the observable "path of the moon" into 27 nakṣatras, but adopted also the Graeco-Roman division into twelve equal sections called Rāśi (राशिः), equalling the traditional zodiacal signs. A rāśi (राशिः) or zodiacal sign is a section of 30° alongside the ecliptic. Since (Greek) antiquity, ecliptic longitudes are typically not counted from one to 359, but are given as "zodiacal sign xy" or "rāśi xy", where 0 ≤ xy ≤ 30.

Therefore, the statement "Mina 2|30" equalling 2.5° of the twelfth Rāśi, means we need to add 11x30=330 and 2.5° to obtain the ecliptic longitude λ=332.5° or dhruvaka=332|30. This is not corrected for precession.

For the vikṣepa (polar latitude measured along the hour circle) is 19|0 N.

Stellarium map of the region in question with tet Psc in the centre and naksatra and rasi displayed (SMH 2025).

If 19.0 is the ecliptic latitude, the star α Peg would have the correct latitude and the longitude of 332.5° would point to a date of measurement in 488/ 489 CE (1200 years prior to Nityānanda' star catalogue). If 19.0 is measured along the hour circle, only zeta Peg would have the correct latitude, but the longitude of 341° in 1639 CE would point to a date of the measurement of 1019 CE.

name ecliptic longitude λ ecliptic latitude β source Indian Name
dhruvaka viksepa
Turaganga 332.5° 19° Nityānanda
α Peg 348.5 19.5 Stellarium (1639) Ajapāda
θ Psc 350.2 9° Stellarium (1639)
ζ Peg 341° 17.75° Stellarium (1639)
γ Peg Ahirbudhnya

Transfer and Transformation of the Constellation

Religion/ Tales/ Mythology

mnemonic tales and cultural significance

Weblinks

References

  1. ↑ Pai and Shylaja, 2021, JOAA, vol 42, 113
Retrieved from "https://xing.fmi.uni-jena.de/mediawiki/index.php?title=Turaganga&oldid=34298"