Turaganga: Difference between revisions

From All Skies Encyclopaedia
Turaganga
No edit summary
 
(14 intermediate revisions by 2 users not shown)
Line 1: Line 1:
{{DISPLAYTITLE:Turagānga}}
{{DISPLAYTITLE:Turagānga}}
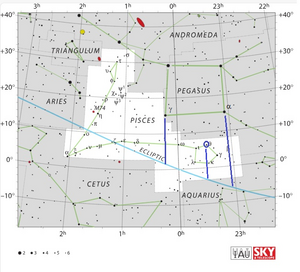
[[File:IdentTuraganga.png|thumb|map for the identification of Turaganga (CC BY B.S. Shylaja).]]

Turagānga () is an Indian name that occurs in a 17th century star catalogue. Most likely, it refers to a body part of the ancient Greek constellation of [[Pegasus]].
Turagānga (तुरगान्ग) is an Indian name that occurs in a 17th century star catalog. Most likely, it refers to a body part of the ancient Greek constellation of [[Pegasus]] and [[Pisces]].


==Concordance, Etymology, History==
==Concordance, Etymology, History==
Turgānga means a body part (anga, ) of the horse (turaga, ).
Turgānga means a body part (anga, अन्ग) of the horse (turaga, तुरग).


===Spelling Variants===
===Spelling Variants===
* Turagānga
* Turagānga
* Turangaamsa
* Turangaasa


===Origin of Constellation===
===Origin of Constellation===
The name is listed in a 17th century star catalogue by Nityānanda in the work ''Siddhāntarāja'' (1639 CE).<ref>Pai and Shylaja, 2021, JOAA, vol 42, 113</ref>
The name is listed in a 17th century star catalogue by Nityānanda in the work ''Siddhāntarāja'' (1639 CE).<ref>Pai and Shylaja, 2021, JOAA, vol 42, 113</ref>


The verse provides the coordinates with numbers coded as sārdhadvaya (two and a half) and gobhūmi (19)
The verse provides the coordinates with numbers coded as ''sārdhadvaya'' (two and a half) and ''gobhūmi'' (19) <blockquote>Half of a degree added to two degrees 2|30 [is one of the coordinates of] the star Turagānga

Half of a degree added to two degrees 2|30 [is one of the coordinates of] the star Turagānga which shines with second order brightness along the north [latitude] as nineteen degrees 19|0.
which shines with second order brightness along the north [latitude] as nineteen degrees 19|0.</blockquote>It is mentioned in the twelfth Rāśi (राशिः), Mina (Pisces).

Since the Greek period in the fourth century CE, Indian astral science used not only the older (Vedic) division of the observable "path of the moon" into 27 nakṣatras, but adopted also the Graeco-Roman division into twelve equal sections called Rāśi (राशिः), equaling the traditional zodiacal signs. A rāśi (राशिः) or zodiacal sign is a section of 30° alongside the ecliptic. Since (Greek) antiquity, ecliptic longitudes are typically not counted from one to 359, but are given as "zodiacal sign ''xy''" or "rāśi ''xy''", where 0 ≤ ''xy'' ≤ 30.


It is grouped in to Mina (Pisces); the 12 zodical rasis are used as divisions of 30 degrees along the ecliptic and grouped by the same name. Longitude measures are provided from 0 to 30 within the rasi. Therefore, we need to add 330 to the coordinate so that dhruvaka (polar longitude, measured along the ecliptic) is 332|30. This is not corrected for precession. The vikṣepa (polar latitude measured along the hour circle) is 19|0 N.
Therefore, the statement "Mina 2|30" equalling 2.5° of the twelfth Rāśi, means we need to add 11x30=330 and 2.5° to obtain the ecliptic longitude ''λ''=332.5° or ''dhruvaka''=332|30. This is not corrected for precession.


For the ''vikṣepa'' (polar latitude measured along the hour circle) is 19|0 N.
Stellarium gives the value 350 degrees for the same epoch. The difference can be attributed to the precession correction.
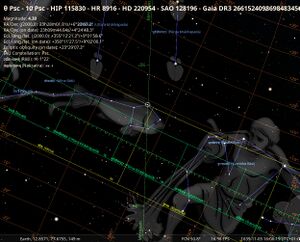
[[File:TetPsc+alfPeg stellarium.jpg|thumb|Stellarium map of the region in question with tet Psc in the centre and naksatra and rasi displayed (SMH 2025).]]
For fixing the coordinates we use the nearest bright stars identified without ambiguity as shown in the chart - Ajapāda Alpha Pegasus and Ahirbudhnya Gamma Pegasus.
If 19.0 is the ecliptic latitude, the star α Peg would have the correct latitude and the longitude of 332.5° would point to a date of measurement in 488/ 489 CE (1200 years prior to Nityānanda' star catalogue). If 19.0 is measured along the hour circle, only ζ Peg would have the correct latitude, but the longitude of 341° in 1639 CE would point to a date of the measurement of 1019 CE.
{| class="wikitable"
|+
!
! colspan="3" |in 1639
!
!
|-
! rowspan="2" |name
!ecliptic longitude λ
!ecliptic latitude β
!β (RA)
! rowspan="2" |source
! rowspan="2" |Indian Name
|-
!''dhruvaka''
!
!''viksepa''
|-
|Turaganga
|332.5°
|
|19°
|Nityānanda
|
|-
|
|
|
|
|
|
|-
|α Peg
|348.5
|19.5
|21° 15'
|Stellarium (1639)
|Ajapāda
|-
|θ Psc
|350.2
|9°
|9° 45'
|Stellarium (1639)
|
|-
|ζ Peg
|341°
|17.75°
|19°
|Stellarium (1639)
|
|-
|γ Peg
|4.1°
|
|13° 40'
|
|Ahirbudhnya
|-
|ι Psc
|352.6°
|
|7° 50'
|
|
|}
Shylaja proposes the identification of "Turangana" with θ Psc or ι Psc. She checked another manuscript with solved examples. It gives the precession correction as 18 degrees for 1620 CE. So without bothering about the errors in ''dhruvaka'' and ''viksepa'', if she simply adds the precession correction it fits with theta Piscium.


However, the text seems to be erroneous, as it gives the difference in coordinates (which does not depend on precession) with errors of 6° to 10°. This lets us doubt the reliability of this text.


===Transfer and Transformation of the Constellation===
===Transfer and Transformation of the Constellation===

Latest revision as of 16:17, 10 November 2025

map for the identification of Turaganga (CC BY B.S. Shylaja).

Turagānga (तुरगान्ग) is an Indian name that occurs in a 17th century star catalog. Most likely, it refers to a body part of the ancient Greek constellation of Pegasus and Pisces.

Concordance, Etymology, History

Turgānga means a body part (anga, अन्ग) of the horse (turaga, तुरग).

Spelling Variants

  • Turagānga
  • Turangaamsa

Origin of Constellation

The name is listed in a 17th century star catalogue by Nityānanda in the work Siddhāntarāja (1639 CE).[1]

The verse provides the coordinates with numbers coded as sārdhadvaya (two and a half) and gobhūmi (19)

Half of a degree added to two degrees 2|30 [is one of the coordinates of] the star Turagānga which shines with second order brightness along the north [latitude] as nineteen degrees 19|0.

It is mentioned in the twelfth Rāśi (राशिः), Mina (Pisces).

Since the Greek period in the fourth century CE, Indian astral science used not only the older (Vedic) division of the observable "path of the moon" into 27 nakṣatras, but adopted also the Graeco-Roman division into twelve equal sections called Rāśi (राशिः), equaling the traditional zodiacal signs. A rāśi (राशिः) or zodiacal sign is a section of 30° alongside the ecliptic. Since (Greek) antiquity, ecliptic longitudes are typically not counted from one to 359, but are given as "zodiacal sign xy" or "rāśi xy", where 0 ≤ xy ≤ 30.

Therefore, the statement "Mina 2|30" equalling 2.5° of the twelfth Rāśi, means we need to add 11x30=330 and 2.5° to obtain the ecliptic longitude λ=332.5° or dhruvaka=332|30. This is not corrected for precession.

For the vikṣepa (polar latitude measured along the hour circle) is 19|0 N.

Stellarium map of the region in question with tet Psc in the centre and naksatra and rasi displayed (SMH 2025).

If 19.0 is the ecliptic latitude, the star α Peg would have the correct latitude and the longitude of 332.5° would point to a date of measurement in 488/ 489 CE (1200 years prior to Nityānanda' star catalogue). If 19.0 is measured along the hour circle, only ζ Peg would have the correct latitude, but the longitude of 341° in 1639 CE would point to a date of the measurement of 1019 CE.

in 1639
name ecliptic longitude λ ecliptic latitude β β (RA) source Indian Name
dhruvaka viksepa
Turaganga 332.5° 19° Nityānanda
α Peg 348.5 19.5 21° 15' Stellarium (1639) Ajapāda
θ Psc 350.2 9° 9° 45' Stellarium (1639)
ζ Peg 341° 17.75° 19° Stellarium (1639)
γ Peg 4.1° 13° 40' Ahirbudhnya
ι Psc 352.6° 7° 50'

Shylaja proposes the identification of "Turangana" with θ Psc or ι Psc. She checked another manuscript with solved examples. It gives the precession correction as 18 degrees for 1620 CE. So without bothering about the errors in dhruvaka and viksepa, if she simply adds the precession correction it fits with theta Piscium.

However, the text seems to be erroneous, as it gives the difference in coordinates (which does not depend on precession) with errors of 6° to 10°. This lets us doubt the reliability of this text.

Transfer and Transformation of the Constellation

Religion/ Tales/ Mythology

mnemonic tales and cultural significance

Weblinks

References

  1. ↑ Pai and Shylaja, 2021, JOAA, vol 42, 113
Retrieved from "https://xing.fmi.uni-jena.de/mediawiki/index.php?title=Turaganga&oldid=34412"